NodeJS
Memoization in JavaScript
Need technical help?
Our experts will get back to you within 24 hours.
What is memoization?
Memoization is a programming optimization approach that increases the speed and efficiency of applications. It accomplishes this by saving computation results in a cache, which it then retrieves the next time it's required rather than computing it from scratch.
In other words, it is about caching the result of a function and making the function check each time whether the required computation is cached before actually computing it.
How Does Memoization Work?
JavaScript Memoization mainly depends on two concepts:
Closure
High-order function
Here’s how the factorial function works without memoization in JavaScript:
We're going to clarify this mumbo jumbo by using the old Fibonacci sequence as our example.
Beginning with ‘one or a zero’ then a one and it is carried forward all as defined in the rule which states that each number or an individual Fibonacci number is equivalent to the sum total of the two preceding numbers.
It looks like this:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
For example, let there be a necessity for developing a g(x) that will calculate the given value of the element of the Fibonacci sequence equal to x. Given that every element is the sum of the previous two, a recursive solution might be the following:
const fib = n => { if (n <= 1) return 1 return fib(n - 1) + fib(n - 2)} If you do not know what recursion means, it is when a function calls itself, of course, we need to add a condition to stop an infinite cycle (if (n <= 1)).
If we call our function like fib(5), behind the scenes our function would execute like this:
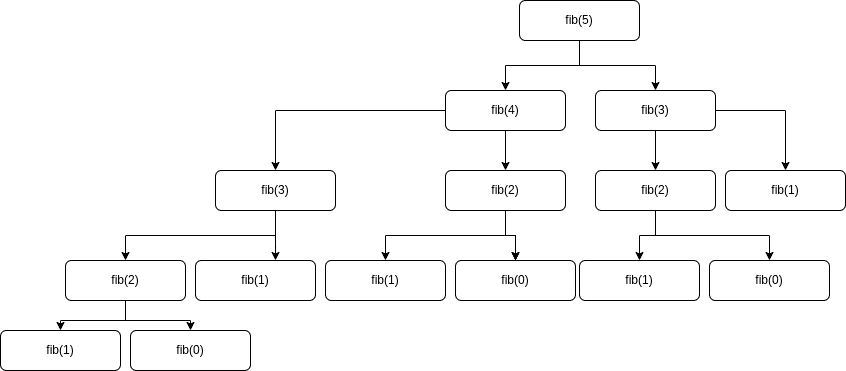
See that we're executing fib(0), fib(1), fib(2) and fib(3) multiple times. Well, that's exactly the kind of problem memoization helps to solve.
With memoization, there's no need to recalculate the same values once and again – we just store each computation and return the same value when required again.
Implementing memoization, our function would look like this:
const fib = (n, memo) => { memo = memo || {} if (memo[n]) return memo[n] if (n <= 1) return 1 return memo[n] = fib(n-1, memo) + fib(n-2, memo)}
What we're doing first is checking if we've received the memo object as a parameter. If we didn't, we set it to be an empty object:
memo = memo || {}
Then, we check if the memo contains the value we're receiving as a param within its keys. If it does, we return that. Here's where the magic happens. No need for more recursion once we have our value stored in memo. =)
if (memo[n]) return memo[n]
If we don't have the value in memo yet, we call fib again, but now passing memo as parameter, so the functions we're calling will share the same memoized values we have in the "original" function. Notice that we add the final result to the cache before returning it.
return memo[n] = fib(n-1, memo) + fib(n-2, memo)
And that's it! With two lines of code we've implemented memoization and significantly improved the performance of our function!
Why is memoization useful?
Memorization is useful since it can significantly increase a function's speed.This checks whether the output is saved for a specific input to avoid having to recompute the output every time the function is called with a certain input.
Code might also be easier to read and comprehend if it is memorized.
The original function can remain as its own object and continue to do its best work without being cluttered by caching code because the caching logic is isolated from it.
Ready to transform your business with our technology solution? Contact Us today to Leverage Our NodeJS Expertise.
0
NodeJS
